Learning circulant sensing kernels

Yangyang Xu, Wotao Yin, and Stanley Osher

Background

In signal acquisition, Toeplitz and circulant matrices are widely used as sensing operators. They correspond to discrete convolutions and are easily or even naturally realized in various applications. For compressive sensing, recent work has used random Toeplitz and circulant sensing matrices and proved their eﬃciency in theory, by computer simulations, as well as through physical optical experiments.

Learn the sensing kernel

One condition for sparse signal recovery from compressive sensing is incoherence between sensing matrix and sparsifying matrix. Given a sparsifying matrix or dictionary 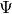Psi , our method aims at learning a circulant sensing matrix/operator to achieve low coherence.

We use circulant matrix/operator is due to signal acquisition consideration particular for large-scale data. A circulant matrix can be written as 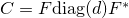$C=Fmathrm{diag}(d)F^*$ , where 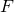is discrete Fourier matrix, so performing 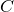to a signal can be realized by a fast Fourier transform (FFT), an inverse FFT, and some component-wise multiplication. Similar argument applies to 2D circulant operator 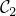$mathcal{C}_2$ by noting it can be written as 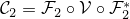$mathcal{C}_2=mathcal{F}_2circmathcal{V}circmathcal{F}_2^*$ , where 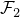$mathcal{F}_2$ is a 2D Fourier transform.

For one-dimensional signal, our method learns a partial circulant matrix by solving

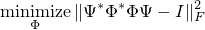
$mathop{mathrm{minimize}}_Phi |Psi^*Phi^*PhiPsi-I|_F^2$

where 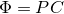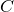Phi=PC , is a circulant matrix, and 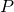is a row-selecting matrix.

For two-dimensional signal, it learns a partial circulant operator by solving

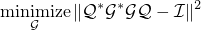
$mathop{mathrm{minimize}}_{mathcal{G}} |mathcal{Q}^*mathcal{G}^*mathcal{G}mathcal{Q}-mathcal{I}|^2$

where 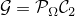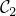$mathcal{G}=mathcal{P}_Omegamathcal{C}_2$ , $mathcal{C}_2$ is a 2D circulant operator, and 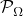$mathcal{P}_Omega$ is a downsampling operator.

The above learning processes are carried out in two steps. The first step learns a circulant matrix/operator, and the second step learns a downsampling matrix/operator. Learning a circulant matrix/operator is equivalent to learning a kernel, and thus it can be easily done. The two steps can be repeated many times. However, the optimization problem about the downsamplers is difficult. We only perform the two steps one time. 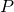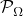One can also choose or $mathcal{P}_Omega$ randomly, which works well on signals without dominating frequency.

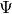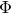In addition, we learn Psi and Phi simultaneously by alternatively updating them. The coupled learning method can be found in Algorithm 2 of our paper.

Selected numerical results

Results of tests using Gaussian random basis (left) and Fourier basis (right) as the sparsify basis

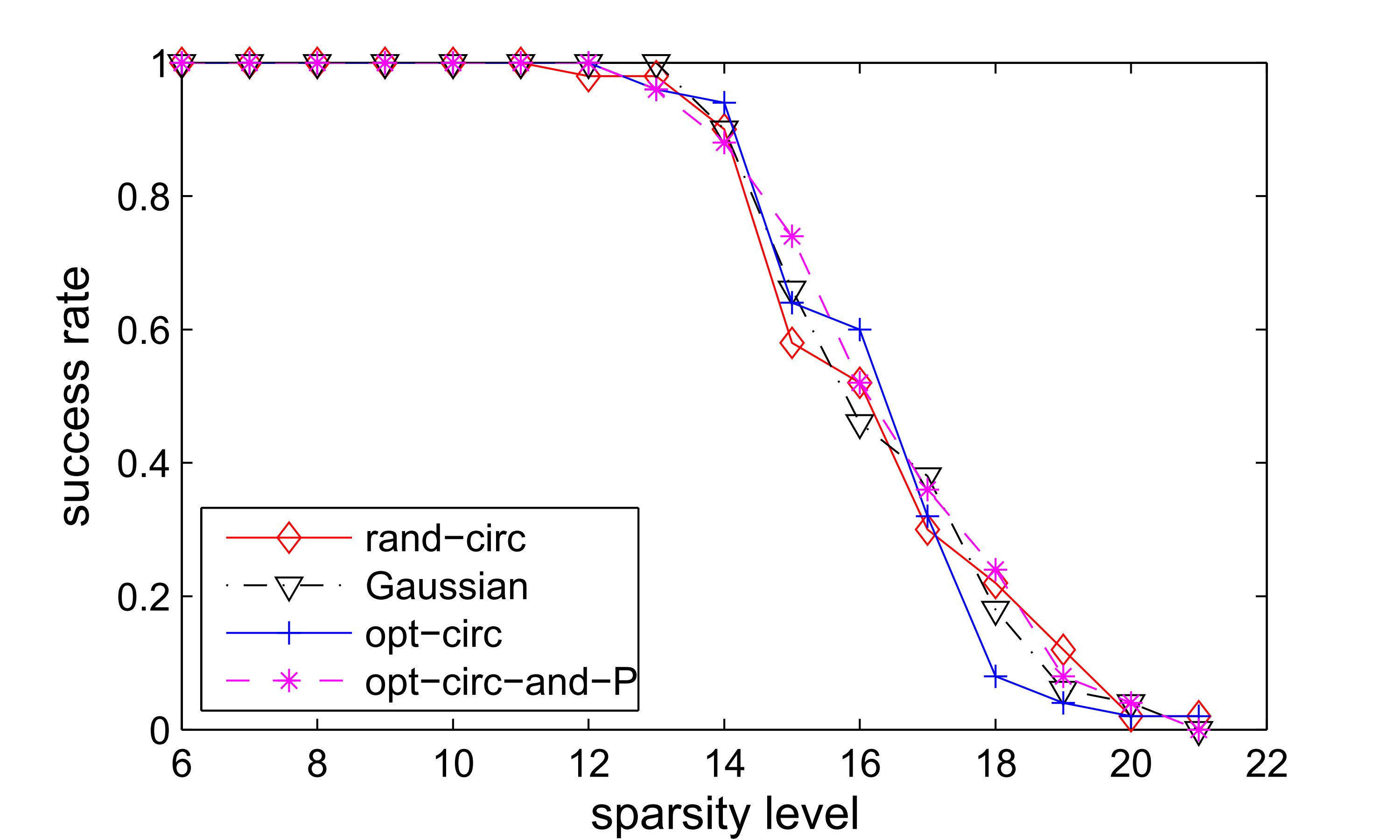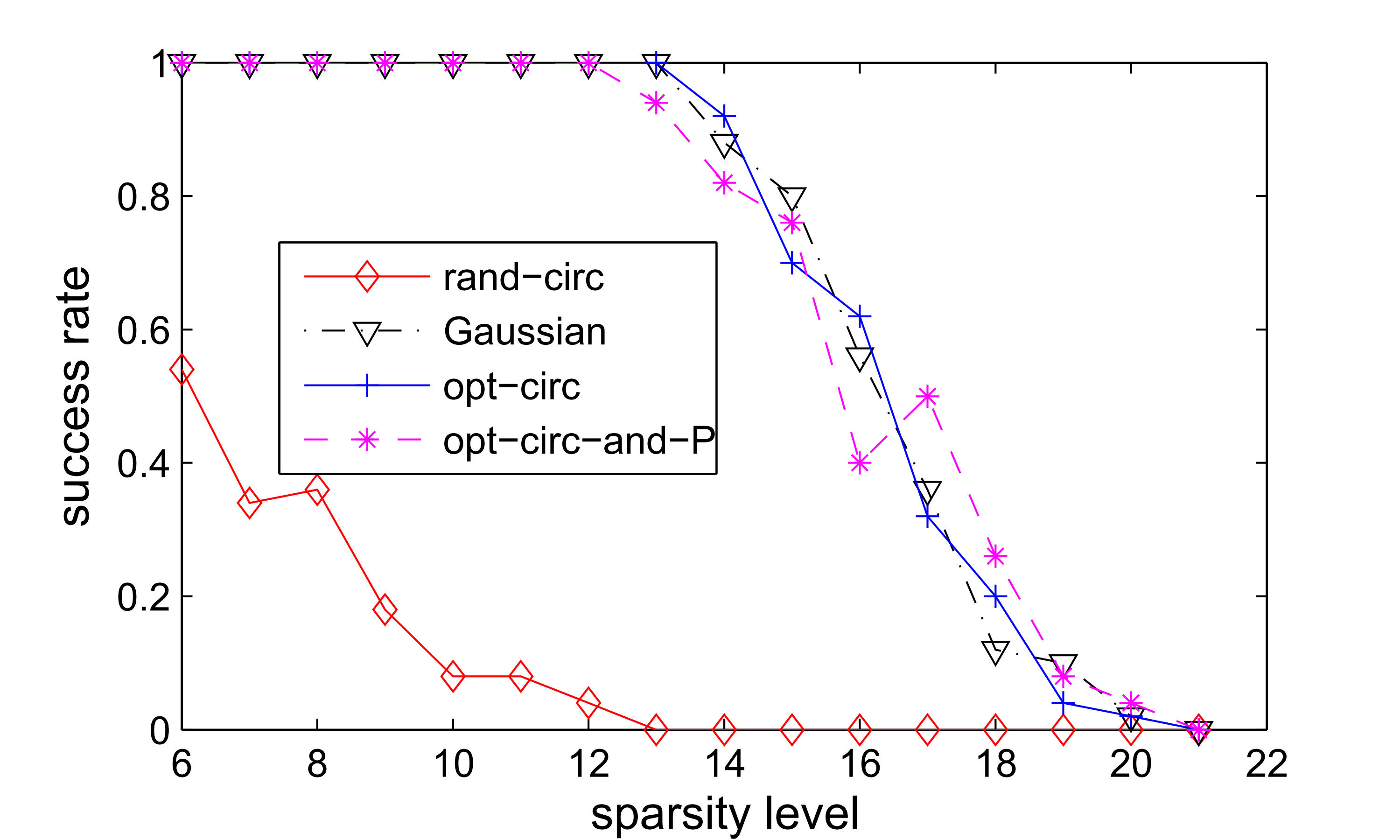Results of real image tests using the images’ 8x8 patches to form dictionaries (left: 16/64 measurements; right: 24/64 measurments)

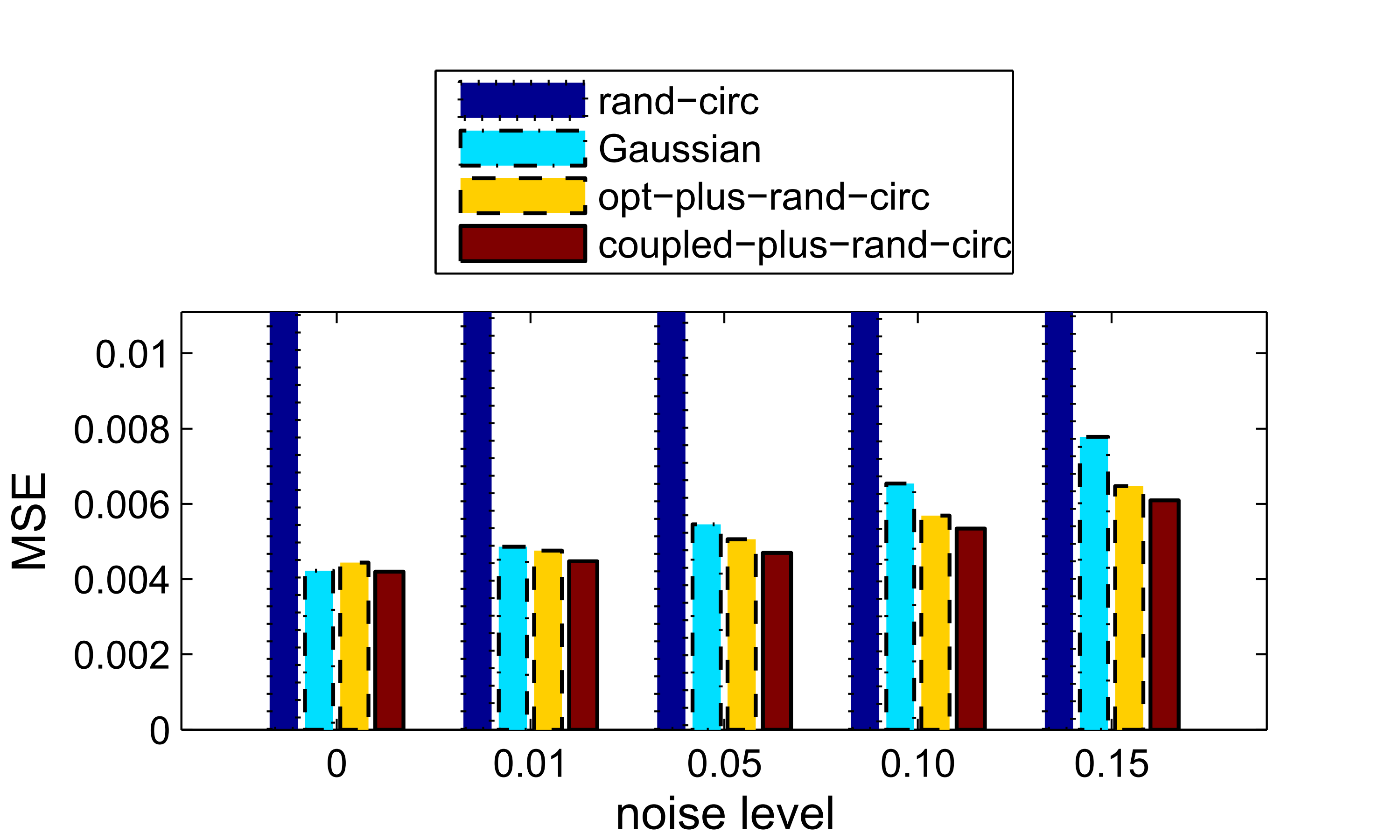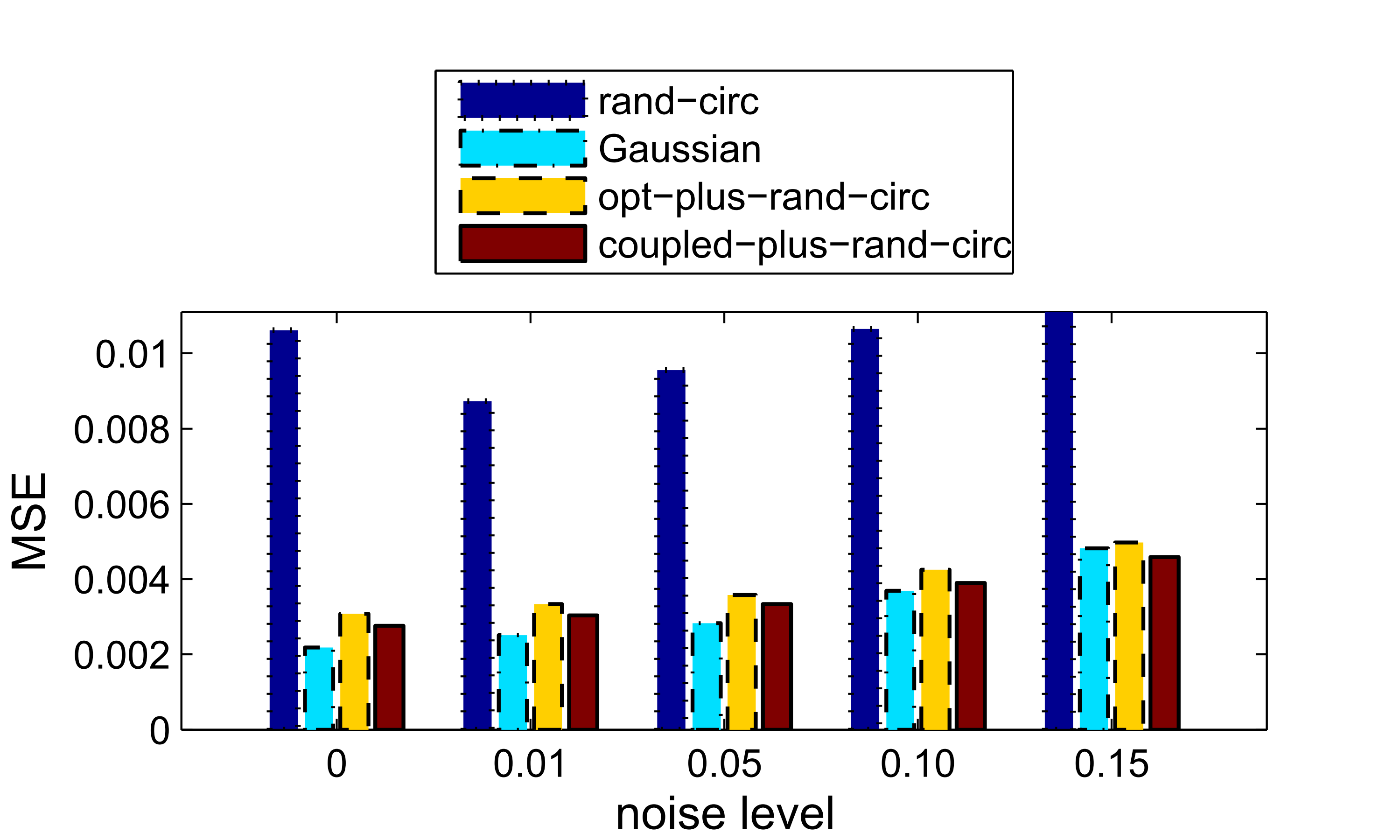Matlab codes

1D test

a test of 1D signal recovery with synthetic dictionaries and a randomly generated sparse signal

2D test

a test that illustrates how to apply a 2D circulant operator to image patches and recover a 2D image from circulant measurements

Fullsize recovery

a test that demonstrates image recovery using a fullsize sensing operator and dictionary; see how to form an image-size dictionary

download code

Citation

Y. Xu, W. Yin, and S. Osher. Learning circulant sensing kernels. Inverse Problems and Imaging, 8(3), 901–923.