Contents

clear; close all;
rand('state',2013); randn('state',2013);

m = 64; % number of rows of sensing matrices
n = 512; % number of columns of sensing matrices

testnum = 50; % total number of independent runs

Psi = dftmtx(n)/sqrt(n); % Fourier basis

suc = zeros(2,6); % to record successful recovery

for k = 6:3:21 % sparsity level
    for num = 1:testnum

generate a sparse signal

        xs = zeros(n,1); % xs is the true signal
        xs(randsample(n,k)) = randn(k,1); % generate a k-sparse signal
        xs = xs/norm(xs); % normalize the signal
        xstart = randn(n,1); % randomly generate a starting point for yall1

generate a random circulant matrix

        v = randn(1,n)+1i*randn(1,n); % generate a random kernel
        C = gallery('circul',v); % generate a circulant matrix
        p = randperm(n);
        Phi = C(p(1:m),:); % select m rows at random
        % normalize the sensing matrix
        for i=1:n
            Phi(:,i) = Phi(:,i)/norm(Phi(:,i));
        end

        % specify parameters for yall1
        A = Phi*Psi;        b = A*xs;
        opts = [];      opts.tol = 5e-8;        opts.x0 = xstart;

        % call yall1
        x = yall1(A,b,opts);

        % record successful recovery of random circulant
        if norm(x-xs)/norm(xs) < 1e-4
            suc(1,k/3-1) = suc(1,k/3-1)+1;
        end

learn circulant matrix

        % form the quadratic program to get the optimized kernel
        % see formula (3.3) in our paper
        F = dftmtx(n)/sqrt(n); % discreate Fourier matrix
        B = F'*Psi*Psi'*F; Bsq = B.*conj(B); dB = diag(B);
        Bsq = (Bsq+Bsq')/2;
        quadopts = optimset('Algorithm','active-set',...
                'Display','off');

        % call Matlab function quadprog to solve the formed quadratic
        % program
        dsq = quadprog(Bsq,-dB,[],[],[],[],zeros(n,1),[],[],quadopts);

        d = sqrt(dsq).*exp(2*1i*pi*rand(n,1)); % generate the phase at random
        C = F*diag(d)*F'; % get the learned circulant matrix

        Phi = C(p(1:m),:); % select m out of n rows

        % normalize the sensing matrix
        for i=1:n
            Phi(:,i) = Phi(:,i)/norm(Phi(:,i));
        end

        % specify the parameters for yall1
        A = Phi*Psi;        b = A*xs;
        opts = [];      opts.tol = 5e-8;        opts.x0 = xstart;

        % call yall1
        x = yall1(A,b,opts);

        % record successful recovery of optimized circulant
        if norm(x-xs)/norm(xs) < 1e-4;
            suc(2,k/3-1) = suc(2,k/3-1)+1;
        end;

    end
end

Reporting

suc = suc/testnum;
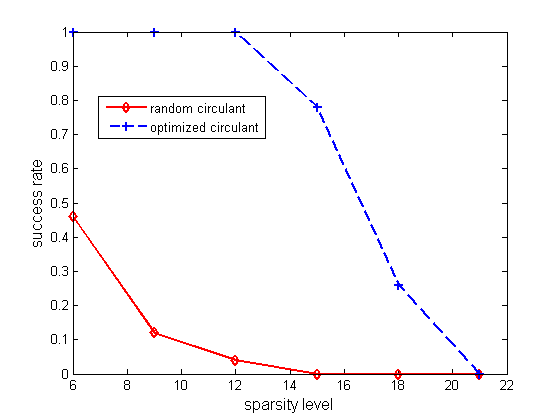
plot(6:3:21,suc(1,:),'r-d','linewidth',2)
hold on;
plot(6:3:21,suc(2,:),'b--+','linewidth',2)
legend('random circulant','optimized circulant','location','best');
xlabel('sparsity level','fontsize',12);
ylabel('success rate','fontsize',12);

Published with MATLAB® 7.11