Alternating proximal gradient method for dictionary learning

Yangyang Xu and Wotao Yin

Background

Dictionary learning has been very popular and shown efficient for many tasks such as image inpainting, image deblurring, super-resolution, and classification. Various algorithms have been proposed for dictionary learning. Famous examples have KSVD $^{[1]}$ , and the online dictionary learning method $^{[2]}$ . Both of them have been demonstrated to work well in practice. However, their convergence results have not been well established.

Our method

We apply the method proposed in our paper to the biconvex dictionary learning model $^{[2]}$

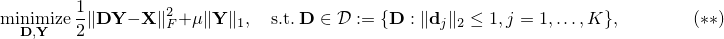
$mathop{mathrm{minimize}}_{mathbf{D},mathbf{Y}}frac{1}{2}|mathbf{D}mathbf{Y}-mathbf{X}|_F^2+mu|mathbf{Y}|_1,quadmathrm{s.t.} mathbf{D}inmathcal{D}:={mathbf{D}:|mathbf{d}_j|_2le 1, j=1,ldots,K},qquadqquad (**)$

where $mathbf{X}=[mathbf{x}_1,ldots,mathbf{x}_p]$ is a given training dataset. Our algorithm iteratively applies the following two updates

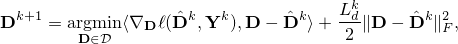
$mathbf{D}^{k+1}=mathop{mathrm{argmin}}_{mathbf{D}inmathcal{D}}langle nabla_{mathbf{D}}ell(hat{mathbf{D}}^k,mathbf{Y}^k),mathbf{D}-hat{mathbf{D}}^krangle + frac{L_d^k}{2}|mathbf{D}-hat{mathbf{D}}^k|_F^2,$

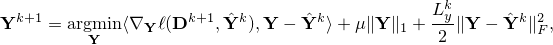
$mathbf{Y}^{k+1}=mathop{mathrm{argmin}}_{mathbf{Y}}langle nabla_{mathbf{Y}}ell(mathbf{D}^{k+1},hat{mathbf{Y}}^k),mathbf{Y}-hat{mathbf{Y}}^krangle + mu|mathbf{Y}|_1 + frac{L_y^k}{2}|mathbf{Y}-hat{mathbf{Y}}^k|_F^2,$

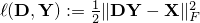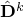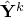where $ell(mathbf{D},mathbf{Y}):=frac{1}{2}|mathbf{D}mathbf{Y}-mathbf{X}|_F^2$ , $hat{mathbf{D}}^k$ and $hat{mathbf{Y}}^k$ are some extrapolated points, and 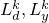L_d^k, L_y^k are Lipschitz constants.

Both the above two updates have closed form solutions and thus the algorithm is very easy to implement. In addition, the extrapolation technique can greatly speed up the convergence. Moreover, the algorithm provably converges to a stationary point of ().

Numerical results

We randomly generate a dictionary 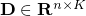$mathbf{D}inmathbf{R}^{ntimes K}$ with 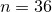fixed. Then let 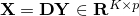$mathbf{X}=mathbf{D}mathbf{Y}inmathbf{R}^{Ktimes p}$ , where each column of 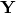has Gaussian randomly generated nonzeros. Each atom 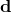of 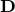is regarded successfully recovered if 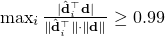$max_ifrac{|hat{mathbf{d}}_i^topmathbf{d}|}{|hat{mathbf{d}}_i^top|cdot|mathbf{d}|}ge 0.99$ , where is the recovered dictionary. The following table shows the time (in second) and recovery rates by our algorithm (Algorithm 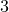in our paper), KSVD and the online dictionary learning method on randomly generated data. Our algorithm performs the best.

Citation

Y. Xu and W. Yin. A fast patch-dictionary method for whole-image recovery. Inverse Problems and Imaging, 10(2), 563–583, 2016.

References

$^{[1]}$ . M. Aharon, M. Elad, and A. Bruckstein. KSVD: an algorithm for designing overcomplete dictionaries for sparse representation, IEEE Transactions on Signal Processing, 54(2006), pp. 4311–4322.

$^{[2]}$ . J. Mairal, F. Bach, J. Ponce, and G. Sapiro. Online dictionary learning for sparse coding, in Proceedings of the 26th Annual Iternational Conference on Machine Learning, ACM, 2009, pp. 689–696.