ADMM for the SDP relaxation of the QAP

Danilo E. Oliveira, Henry Wolkowicz and Yangyang Xu

Background

The quadratic assignment problem (QAP) is one of the hardest NP-hard discrete optimization problems. The semidefinite programming (SDP) relaxation has proven to be extremely strong for QAP by lifting the variable [1]. However, the SDP relaxation for the QAP becomes very large, and traditional methods such as the interior-point method can hardly solve problems of even medium size, say 30.

We reformulate and also strengthen the relaxation model in [1] by splitting variables and adding more constraints. Then we employ the alternating direction method of multiplier (ADMM) to solve the strengthened model with or without an additional low-rank constraint. We obtain very sharp lower bound on benchmark datasets within much shorter time compared to the best existing method.

Notation and our method

The QAP problem can be formulated as

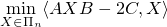
$min_{XinPi_n} langle AXB-2C, X rangle$

where 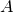and 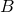are real symmetric matrices, 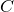is a real matrix, and 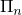Pi_n denotes the set of 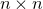ntimes n permutation matrices. By lifting variable, [1] relaxed the original QAP problem into

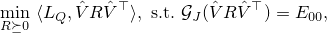
$min_{Rsucceq 0} langle L_Q, hat{V}Rhat{V}^toprangle, ~mathrm{s.t.}~mathcal{G}_J(hat{V}Rhat{V}^top)=E_{00},$

where 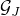$mathcal{G}_J$ is a sampling operator (also called gangster operator) picking the elements in the index set 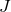, 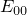$E_{00}$ is a matrix with all zeros except the top-left one, 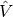hat{V} is a basis matrix (see our report), and

$L_Q=left[begin{array}{cc}0 & -mathrm{vec}(C)^top-mathrm{vec}(C) & Botimes Aend{array}right].$

We introduce another variable 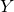and enforce 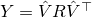$Y= hat{V}Rhat{V}^top$ and also restrict 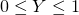0le Yle 1 , resulting in the following model

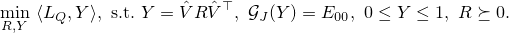
$min_{R, Y} langle L_Q, Yrangle, mathrm{s.t.} Y= hat{V}Rhat{V}^top, mathcal{G}_J(Y)=E_{00}, 0le Yle 1, Rsucceq 0.$

Then the ADMM method is applied to solve the above model with or without the rank-one constraint 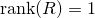mathrm{rank}(R)=1 . Due to the introducing of 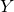, every step in the ADMM method has closed form solution, and numerically ADMM is very efficient on solving our problem.

Numerical results

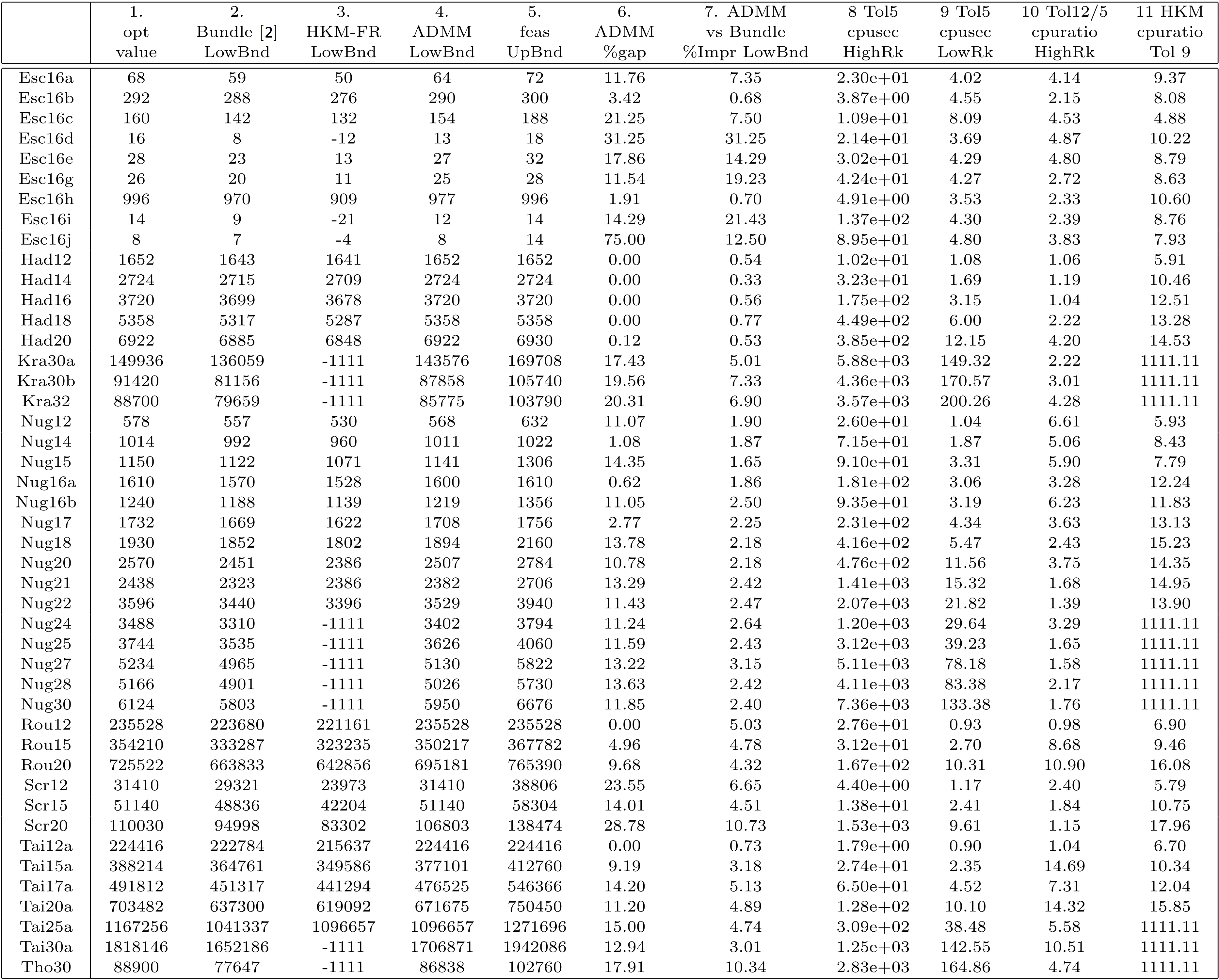
We test our method on 45 benchmark QAP instances. Compared to the best existing lower bound (column 2 by Bundle method [2]), our method improves the lower bound on every instance. In addition, our method is very fast, in particular when there is a low-rank constraint (column 9).

Matlab code

Download the code

Citation

D. Oliveira, H. Wolkowicz, and Y. Xu. ADMM for the SDP relaxation of the QAP. Mathematical Programming Computation, 10(4), pp. 631–658, 2018.

References

$^{[1]}$ . Q. Zhao, S.E. Karisch, F. Rendl, and H. Wolkowicz. Semidefinite programming relaxations for the quadratic assignment problem, J. Combinatorial Optimization, 2(1): 71–109, 1998.

$^{[2]}$ . F. Rendl and R. Sotirov. Bounds for the quadratic assignment problem using the bundle method. Math. Program., 109 (2–3, Ser. B): 505–524, 2007